La descrizione della tecnica e soprattutto il vademecum alla lettura dei sondaggi li trovate qui.
Dato che la serie temporale inizia ad essere lunghetta, metto anche qualche zoom sugli ultimi tempi.
Inoltre, sempre tenendo conto che in politica 2+2 a volte fa 3, altre fa 5, e visto che la destra ha trovato (no, chi l'avrebbe mai detto? Ricordate quando Salvini e Meloni infamavano Berlusconi e Forza Italia?) un "accordo", aggiungo il listone Forza Italia + Lega Nord + Fratelli d'Italia.
Questa invece zoomma sugli ultimi 12 mesi
Ultimi 6 mesi
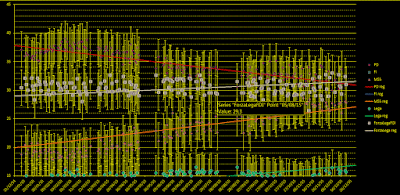
Ultimi 3 mesi
Ultimo mese
NOVITÀ
Visto che la legge elettorale prevede il ballottaggio tra le prime due liste, voglio azzardare una nuova stima: le probabilità di ballottaggio.
Sperando che lo spirito del Teorema del Limite Centrale mi accompagni, considero come stime finali delle percentuali che le liste maggiori (PD, Destra, M5S) prenderebbero se si votasse domani l'ultimo valore della retta di regressione. Ipotizzo poi che tale stima sia una variabile aleatoria distribuita secondo distribuzione normale a media pari a tale valore e deviazione standard pari all'incertezza a priori che dichiaro, ovvero ±1.5%. Si otterrebbe dunque come stime finali:
- Destra: (31.5 ± 1.5)%
- PD: (30.9 ± 1.5)%
- M5S: (27.1 ± 1.5)%
Andando a calcolare l'integrale delle code sovrapposte delle relative gaussiane normalizzate (vedi qui) calcolo le probabilità di ballottaggio.
ATTENZIONE!
Che cos'è una probabilità? È un numero compreso tra 0 e 1 che dice che se si fanno tanti tanti tanti esperimenti indipendenti, i risultati saranno abbastanza allineati alle percentuali. Nel singolo esperimento, però, può succedere di tutto [5].
Ciò detto, le probabilità delle tre possibili combinazioni sono le seguenti:
- Ballottaggio PD vs Destra: 97.34%
- Ballottaggio M5S vs PD: 0.58%
- Ballottaggio Destra vs M5S: 2.08%
Ricordo che comunque il dato della Destra potrebbe essere mal stimato perché i voti che prende una lista composita raramente è pari alla somma dei componenti presi singolarmente.
Ho calcolato, per completezza, la probabilità che una di queste tre liste superi il 40% e dunque non ci sia ballottaggio: la probabilità totale che non ci sia ballottaggio è dell'ordine di 10^-80, ovvero non nulla ma assolutamente trascurabile.
Ho calcolato, per completezza, la probabilità che una di queste tre liste superi il 40% e dunque non ci sia ballottaggio: la probabilità totale che non ci sia ballottaggio è dell'ordine di 10^-80, ovvero non nulla ma assolutamente trascurabile.
Ho linkato il vademecum, ma ci tengo a ripeterlo ché visto che gente che dovrebbe essere giornalista continua a dire stronzate, repetita iuvant.
- i sondaggi sono stime eseguite su un sottoinsieme molto piccolo (in genere 800 o 1000 unità, raramente 1500) della popolazione [1];
- il campione non è scelto a cazzo di cane, ma è scelto con opportune e scientifiche tecniche di dimostrata validità che sono riportate quando si scarica il sondaggio dal sito;
- la gente ha da fare e non è ben disposta a rispondere alle domande perdendo mezz'ora di vita, per cui è normale che per avere 1000 risposte servano 5000-6000 tentativi;
- ogni sondaggista ha dei "numeri magici" con cui corregge la stima, e a volte li usa per portare acqua al suo mulino, altre per migliorare le stime; ma prendendo sondaggi da tutte le fonti dal TgCom a Ballarò la cosa si compensa;
- in quanto stime, i sondaggi sono endemicamente ed ineliminabilmente affetti da incertezza;
- l'incertezza è una stima a priori dell'errore commesso ed è a sua volta una stima affetta da incertezza, ma non è fatta alla cazzo di cane ma anche questa calcolata con tecniche di provata validità scientifica;
- il modo migliore per leggere un dato affetto da incertezza è il seguente [2] : se in un sondaggio a incertezza 3.5% il PD è dato al 30%, significa che c'è una probabilità pari al 95% che il dato reale del PD sia tra 30% + 3.5% e 30% - 3.5%;
- in conseguenza, quando un giornalista coglione, ignorante o in mala fede dice cose tipo "il PD prende, rispetto alla precedente rilevazione, uno +0.3%" sta dicendo una cosa che è scientificamente una cazzata, mentre la dizione sensata in un caso del genere sarebbe "il dato del PD è compatibile con quello della precedente rilevazione";
- esiste una legge matematica per cui, avendo N rilevazioni indipendenti, l'incertezza diminuisce come la radice quadrata di N [3];
- i sondaggi su 500 persone hanno in genere incertezza 4.5%, quelli su 800 persone 3.5%, quelli su 1000 persone 3%, quelli su 1500 2.5% [4];
- facendo la regressione lineare dovrebbe diminuire l'incertezza, ma non conoscendo quanto siano indipendenti i campioni dei vari sondaggi, non mi arrischio a fare a mia volta una stima di incertezza, tuttavia quest'incertezza è certamente minore o uguale a 1.5%.
_________________________________________________________________________
[1] "Popolazione" è un termine tecnico della statistica, nel nostro caso si intendono i circa 50.000.000 di cittadini maggiorenni in possesso dei diritti politici attivi.
[2] Questo modo non è sempre valido, ha delle ipotesi alla base, ma non voglio fare lezioni di statistica che tra l'altro non sarei in grado di fare.
[3] Cioè se ho 16 sondaggi a incertezza 3.5%, combinando i dati e supponendo che siano indipendenti potrei stimare l'incertezza finale in 3.5%/4=0.88%
[4] Coerentemente con quanto detto al punto 9. e spiegato nella nota [3], raddoppiare il campione non dimezza l'incertezza, per dimezzare l'incertezza bisogna quadruplicare il campione.
[5] Se non ci credete, provate a lanciare un dado 6 volte, Difficilmente verrà una volta 1, una volta 2, una volta 3, una volta 4, una volta 5 e un volta 6 come la probabilità (1/6 per ogni numero) vorrebbe. Provate a lanciarlo 500 volte, e i numeri usciranno circa 1/6 delle volte (altrimenti il dado è truccato!).




Nessun commento:
Posta un commento
Libertà assoluta, anche se mi offendi al limite ti rispondo ma non ti censuro